Epitrocoide

Las ecuaciones paramétricas de una curva epitrocoide son:

${\displaystyle x=(R+r)\cos \theta -d\cos \left({R+r \over r}\theta \right)}$

${\displaystyle y=(R+r)\operatorname {sen} \theta -d\operatorname {sen} \left({R+r \over r}\theta \right)}$

donde:

• R es el radio de la circunferencia directriz,
• r el radio de la circunferencia generatriz, y
• d la distancia del punto al centro de la circunferencia generatriz.

Las epitrocoides son una clase general de curvas, entre las cuales encontramos el epicicloide (cuando d = r, es decir, cuando la curva queda determinada por un punto de la circunferencia generatriz) y el caracol de Pascal (cuando R = r, es decir, cuando los dos círculos tienen el mismo radio).

Son epitrocoides, por ejemplo, las órbitas de los planetas según la teoría geocéntrica de Ptolomeo, o el estátor del motor Wankel.

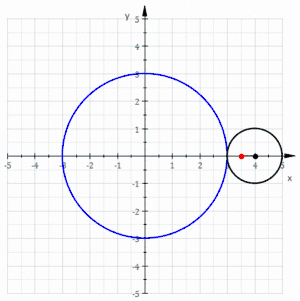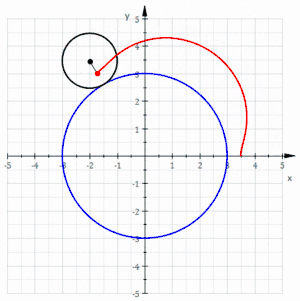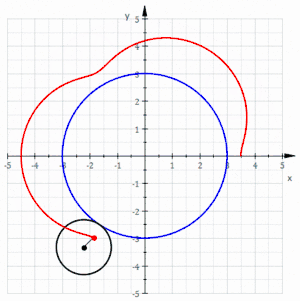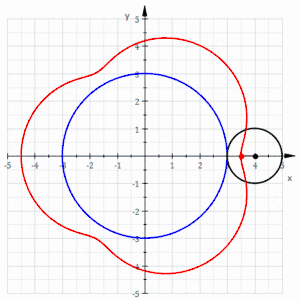La curva roja es un epitrocoide acortada dibujada gracias a un círculo negro rodante sin deslizarse alrededor de un círculo azul (los parámetros son R = 3, r = 1 y d = 0,5)

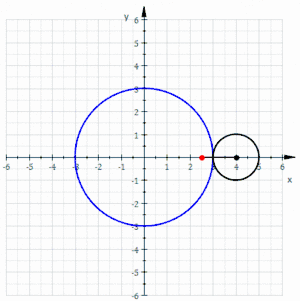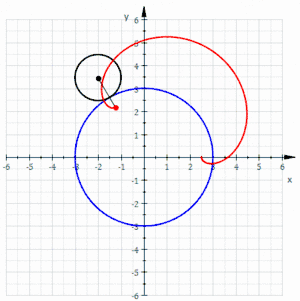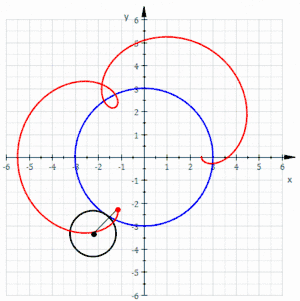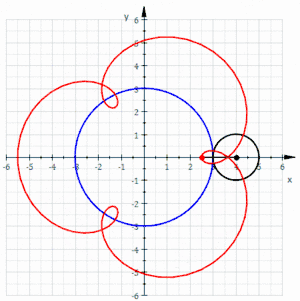La curva roja es un epitrocoide alargada dibujada gracias a un círculo negro rodante sin deslizarse alrededor de un círculo azul (los parámetros son R = 3, r = 1 y d = 1,5)

Curva cíclica

La directriz es una recta
d = r	d < r	d > r
cicloide	trocoide
cicloide normal	cicloide acortada	cicloide alargada

La directriz es una circunferencia
	d = r	d < r	d > r
La generatriz es exterior a al directriz	epicicloide	epitrocoide
	epicicloide normal	epicicloide acortada	epicicloide alargada
La generatriz es interior a al directriz	hipocicloide	hipotrocoide
	hipocicloide normal	hipocicloide acortada	hipocicloide alargada
La directriz es interior a al generatriz	pericicloide	peritrocoide
	pericicloide normal	pericicloide acortada	pericicloide alargada

• Hipotrocoide
• Trocoide

• Weisstein, Eric W. «Epitrochoid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Consultado el 18 de junio de 2008.