Epicicloide
La epicicloide es la curva generada por la trayectoria de un punto perteneciente a una circunferencia (generatriz) que rueda, sin deslizamiento, por el exterior de otra circunferencia (directriz). Es un tipo de ruleta cicloidal.
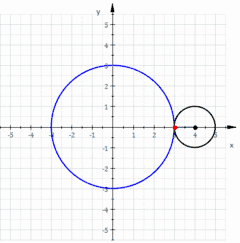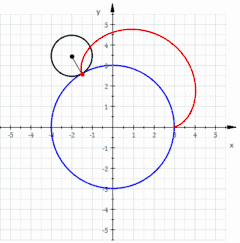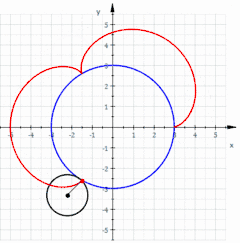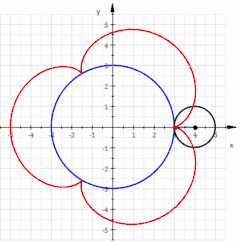
La curva roja es una epicicloide trazada a medida que el pequeño círculo (radio r = 1) gira sobre la circunferencia de un círculo mayor (radio R = 3).
Ecuación
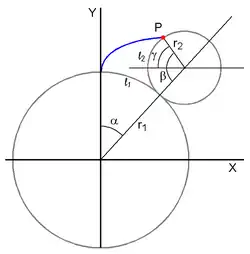
Considerando la figura podemos escribir:
(1)
(2)
con y, además, como la circunferencia rueda sin deslizamiento, los arcos l1 y l2 son iguales, i.e: . De aquí se tiene que
Sustituyendo β y γ en las ecuaciones [1] y [2] tenemos la ecuación paramétrica de la epicicloide:
Ejemplos
- ejemplos de epicicloides
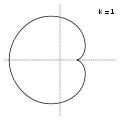 k=1
k=1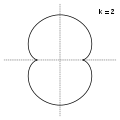 k=2
k=2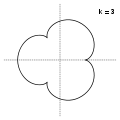 k=3
k=3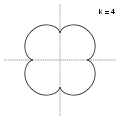 k=4
k=4 k=2,1=21/10
k=2,1=21/10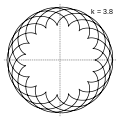 k=3,8=19/5
k=3,8=19/5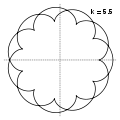 k=5,5=11/2
k=5,5=11/2 k=7,2=36/5
k=7,2=36/5
Curvas cíclicas
La directriz es una recta d = r d < r d > r cicloide trocoide cicloide normal cicloide acortada cicloide alargada
La directriz es una circunferencia d = r d < r d > r La generatriz es exterior a al directriz epicicloide epitrocoide epicicloide normal epicicloide acortada epicicloide alargada La generatriz es interior a al directriz hipocicloide hipotrocoide hipocicloide normal hipocicloide acortada hipocicloide alargada La directriz es interior a al generatriz pericicloide peritrocoide pericicloide normal pericicloide acortada pericicloide alargada
Véase también
Referencias en la Web
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.