En la teoría de sistemas de muchas partículas, las coordenadas de Jacobi se usan con frecuencia para simplificar las fórmulas matemáticas. Estas coordenadas son especialmente comunes en el tratamiento de moléculas poliatómicas y reacciones químicas,^[1] y en mecánica celeste.^[2]

Algoritmo para N cuerpos

Un algoritmo para generar coordenadas de Jacobi para N cuerpos puede basarse en árboles binarios.^[3] Literalmente el algoritmo se describe como sigue:^[3]

Sean m_j y m_k las masas de dos cuerpos que son reemplazados por un nuevo cuerpo de masa virtual M = m_j + m_k.

Las coordenadas x _j y x _k se reemplazan por sus posiciones relativas r_jk =x_j − x_k y por el vector al centro de sus masas R_jk = (m_j q_j + m_kq_k)/(m_j + m_k).

El nodo en el árbol binario correspondiente al cuerpo virtual tiene m_j como rama derecha y m_k como rama izquierda. El orden de las ramas indica el punto de coordenadas relativas desde x'_k a x_j.

Repita esta secuencia para N − 1 cuerpos, o sea los N − 2 cuerpos originales más el nuevo cuerpo virtual.

Un posible conjunto de coordenadas de Jacobi para el problema de los cuatro cuerpos; las coordenadas de Jacobi son r₁, r₂, r₃ y el centro de gravedad R. Véase Cornille.^[4]

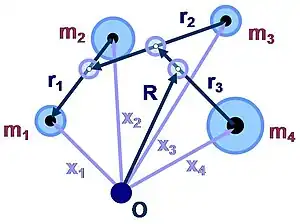
Problema de los cuatro cuerpos

Para el problema de cuatro cuerpos el resultado es:^[4]

${\displaystyle {\boldsymbol {r_{1}=x_{1}-x_{2}}}\ ,}$

${\displaystyle {\boldsymbol {r_{j}}}={\frac {1}{m_{0j}}}\sum _{k=1}^{j}m_{k}{\boldsymbol {x_{k}}}\ -\ {\boldsymbol {x_{j+1}}}\ ,}$

con

${\displaystyle m_{0j}=\sum _{k=1}^{j}\ m_{k}\ .}$

El vector R es el centro de gravedad de todos los cuerpos:

${\displaystyle {\boldsymbol {R}}={\frac {1}{m_{0}}}\sum _{k=1}^{N}\ m_{k}{\boldsymbol {x_{k}}}\$ ;}   ${\displaystyle m_{0}=\sum _{k=1}^{N}\ m_{k}\ .}$

Referencias