Gráfica de ${\displaystyle S_{n}/n}$ (rojo), su desviación típica ${\displaystyle 1/{\sqrt {n}}}$ (azul) y su cota ${\displaystyle {\sqrt {2\log \log n/n}}}$ dada por la ley del logaritmo iterado (verde). Obsérvese la forma aleatoria en que cambia de su cota superior a su cota inferior. Ambos ejes están escalados por una función no lineal (ver detalles en la versión en inglés).

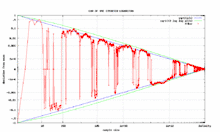
En teoría de la probabilidad, la ley del logaritmo iterado describe la magnitud de las fluctuaciones de un paseo aleatorio. El enunciado original de esta ley se debe a A. Y. Jinchin (1924).^[1] A. N. Kolmogórov dio otra versión en 1929.^[2]

Enunciado

Sean ${\displaystyle \{Y_{n}\}}$ variables aleatorias independientes e idénticamente distribuidas, con media cero y varianza uno. Sea ${\displaystyle S_{n}=Y_{1}+\cdots +Y_{n}}$. Entonces

$${\displaystyle \limsup _{n\rightarrow \infty }{\frac {\pm S_{n}}{\sqrt {2n\log \log n}}}=1}$$

casi seguramente.

Discusión

La ley del logaritmo iterado opera "entre" la ley de los grandes números y el teorema central del límite. Hay dos versiones de la ley de los grandes números (la débil y la fuerte), y afirman que las sumas ${\displaystyle S_{n}}$, escaladas por ${\displaystyle n^{-1}}$, convergen a cero (en probabilidad y casi seguramente, respectivamente):

${\displaystyle {\frac {S_{n}}{n}}\ {\overset {p}{\rightarrow }}\ 0,\qquad {\frac {S_{n}}{n}}\ {\overset {c.s.}{\rightarrow }}\ 0,\qquad {\text{cuando }}\ n\rightarrow \infty .}$

Por otra parte, el teorema central del límite afirma que las sumas ${\displaystyle S_{n}}$, escaladas por ${\displaystyle n^{-1/2}}$, convergen en distribución a una distribución normal estándar. Por la ley cero-uno de Kolmogórov, para cada ${\displaystyle M}$ fijo, la probabilidad del evento ${\displaystyle \limsup _{n}{\frac {S_{n}}{\sqrt {n}}}\geq M}$ es 0 o 1. Pero

${\displaystyle \Pr \left(\limsup _{n}{\frac {S_{n}}{\sqrt {n}}}\geq M\right)\geqslant \limsup _{n}\Pr \left({\frac {S_{n}}{\sqrt {n}}}\geq M\right)=\Pr \left({\mathcal {N}}(0,1)\geq M\right)>0,}$

luego

${\displaystyle \limsup _{n}{\frac {S_{n}}{\sqrt {n}}}=\infty \qquad {\text{con probabilidad 1.}}}$

Un argumento análogo prueba que

${\displaystyle \liminf _{n}{\frac {S_{n}}{\sqrt {n}}}=-\infty \qquad {\text{con probabilidad 1.}}}$

Por tanto, estas cantidades no pueden converger casi seguramente. De hecho, tampoco pueden converger en probabilidad, debido a la igualdad

${\displaystyle {\frac {S_{2n}}{\sqrt {2n}}}-{\frac {S_{n}}{\sqrt {n}}}={\frac {1}{\sqrt {2}}}{\frac {S_{2n}-S_{n}}{\sqrt {n}}}-\left(1-{\frac {1}{\sqrt {2}}}\right){\frac {S_{n}}{\sqrt {n}}}}$

y al hecho de que las variables aleatorias

${\displaystyle {\frac {S_{n}}{\sqrt {n}}}\quad {\text{and}}\quad {\frac {S_{2n}-S_{n}}{\sqrt {n}}}}$

son independientes y convergen en distribución a ${\displaystyle {\mathcal {N}}(0,1).}$

La ley del logaritmo iterado proporciona el factor de escala en el que los dos límites se vuelven diferentes:

${\displaystyle {\frac {S_{n}}{\sqrt {2n\log \log n}}}\ {\xrightarrow {p}}\ 0,\qquad {\frac {S_{n}}{\sqrt {2n\log \log n}}}\ {\stackrel {c.s.}{\nrightarrow }}\ 0,\qquad {\text{cuando}}\ \ n\to \infty .}$

Así, aunque para cualquier ${\displaystyle \epsilon >0}$ fijo la cantidad ${\displaystyle \left|S_{n}/{\sqrt {2n\log \log n}}\right|}$ será menor que ${\displaystyle \epsilon }$ con probabilidad tendiendo a 1, esta cantidad será sin embargo mayor que ${\displaystyle \epsilon }$ para valores de ${\displaystyle n}$ arbitrariamente grandes, casi seguramente; de hecho, esta cantidad visitará los entornos de cualquier punto del intervalo ${\displaystyle (-1,1)}$ para valores de ${\displaystyle n}$ arbitrariamente grandes, casi seguramente.

Referencias