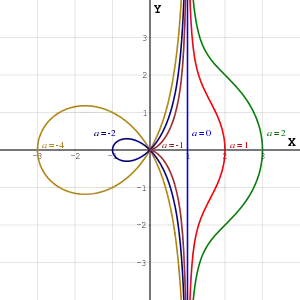
La concoide de de Sluze para algunos valores de a

La(s) concoide(s) de de Sluze son una familia de curvas planas estudiadas en 1662 por el matemático belga René François Walter, barón de Sluze.

Están definidas por la ecuación polar^[1]

${\displaystyle r=\sec \theta +a\cos \theta \,}$

En coordenadas cartesianas, las curvas satisfacen la ecuación implícita

${\displaystyle (x-1)(x^{2}+y^{2})=ax^{2}\,}$

excepto para a=0, la forma implícita presenta un acnodo en (0,0), que no aparece en la forma polar.

Son curvas planas racionales, circulares y cúbicas.

Estas expresiones tienen una asíntota x=1 (para a≠0). El punto más distante de la asíntota es (1+a,0). (0,0) que es un crunodo para a<−1.

El área entre la curva y la asíntota es, para ${\displaystyle a\geq -1}$

${\displaystyle |a|(1+a/4)\pi \,}$

mientras que para ${\displaystyle a<-1}$, el área es

${\displaystyle \left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}-a\left(2+{\frac {a}{2}}\right)\arcsin {\frac {1}{\sqrt {-a}}}.}$

Si ${\displaystyle a<-1}$, la curva tiene un bucle. El área del bucle es

${\displaystyle \left(2+{\frac {a}{2}}\right)a\arccos {\frac {1}{\sqrt {-a}}}+\left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}.}$

Cuatro de los miembros de la familia tienen nombres particulares:

• a =0, recta (asíntota al resto de la familia)
• a =−1, cisoide de Diocles
• a =−2, estrofoide derecha.
• a =−4, trisectriz de Maclaurin

Véase también

• Concoide de Durero
• Curvas

Referencias