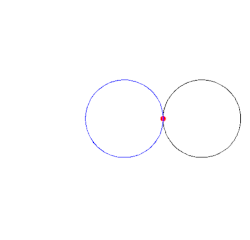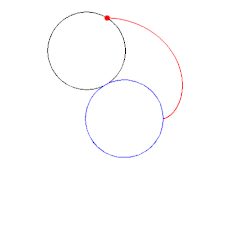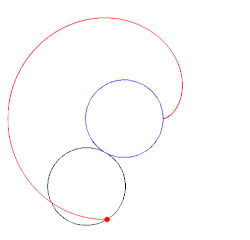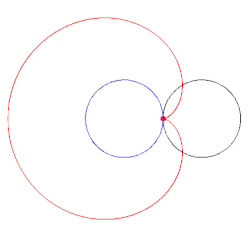
Una cardioide generada por una circunferencia que rueda.

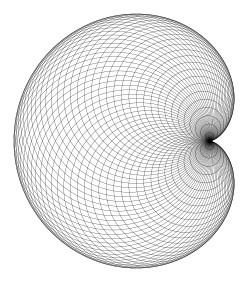
Una cardioide dada como la envoltura de las circunferencias cuyos centros pertenecen a una circunferencia dada y que pasan a través de un punto fijo de una circunferencia dada.

Se llama cardioide a la curva cuya ecuación polar es: ρ=a(1+cos θ), por su semejanza con el dibujo de un corazón.

La cardioide es una curva ruleta de tipo epicicloide, con k=1. También es un caracol de Pascal, cuando 2a=h.

El nombre fue acuñado en 1741^[1] por el matemático italiano de Castillon (1708–1791) pero la curva ya había sido objeto de estudio desde hacía décadas.^[2]

Véase también

• Ruleta
• Caracol de Pascal
• Epicicloide
• Coordenadas polares
• Micrófono cardioide
• Paradoja de la moneda que gira

Notas

• Weisstein, Eric W. «Cardioid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Cardioide.
• La cardioide