Triaquis tetraedro truncado

Triaquis tetraedro truncado
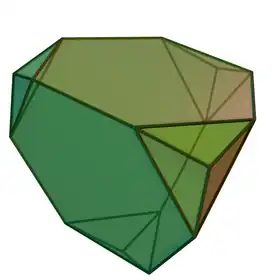	; Imagen del sólido
Tipo	Plesioedro
Caras	4 hexágonos; 12 triángulos isósceles
Aristas	30
Vértices	16
Poliedro dual	16\|Orden-3 triaquis tetraedro truncado
Conway	k3tT
Propiedades
	Figura convexa

En geometría, el triaquis tetraedro truncado es un poliedro convexo formado por 4 hexágonos y 12 triángulos isósceles. Se puede utilizar para teselar el espacio tridimensional, formando un panal triaquis tetraédrico truncado.[1][2]

El triaquis tetraedro truncado es la forma de la celda de Voronoi de los átomos de carbono en el diamante, que se encuentra en la estructura cristalina del diamante cúbico.[3][4] Como celda de Voronoi de un patrón espacial simétrico, es una plesioedro.[5]

Construcción

Panal triaquis tetraédrico truncado

Para rellenar el espacio, el triaquis tetraedro truncado se puede construir de la siguiente manera:

Truncar un tetraedro regular de modo que las caras grandes sean hexágonos regulares.
Agregar un vértice adicional en el centro de cada uno de los cuatro tetraedros más pequeños que se eliminaron, para formar una pirámide sobre cada una de ellas

Véase también

Panal cuarto cúbico
Tetraedro truncado
Triaquistetraedro

Referencias

Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. p. 332. ISBN 978-1568812205.
Grünbaum, B; Shephard, G. C. (1980). «Tilings with Congruent Tiles». Bull. Amer. Math. Soc. 3 (3): 951-973. doi:10.1090/s0273-0979-1980-14827-2.
Föppl, L. (1914). «Der Fundamentalbereich des Diamantgitters». Phys. Z. 15: 191-193.
Conway, John. «Voronoi Polyhedron». geometry.puzzles. Consultado el 20 de septiembre de 2012.
Grünbaum, Branko; Shephard, G. C. (1980), «Tilings with congruent tiles», Bulletin of the American Mathematical Society, New Series 3 (3): 951-973, MR 585178, doi:10.1090/S0273-0979-1980-14827-2..

Datos: Q7839931

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[conway2008-1] Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. p. 332. ISBN 978-1568812205.

[2] Grünbaum, B; Shephard, G. C. (1980). «Tilings with Congruent Tiles». Bull. Amer. Math. Soc. 3 (3): 951-973. doi:10.1090/s0273-0979-1980-14827-2.

[3] Föppl, L. (1914). «Der Fundamentalbereich des Diamantgitters». Phys. Z. 15: 191-193.

[conway2003-4] Conway, John. «Voronoi Polyhedron». geometry.puzzles. Consultado el 20 de septiembre de 2012.

[5] Grünbaum, Branko; Shephard, G. C. (1980), «Tilings with congruent tiles», Bulletin of the American Mathematical Society, New Series 3 (3): 951-973, MR 585178, doi:10.1090/S0273-0979-1980-14827-2..