Rombidodecadodecaedro
En geometría, el rombidodecadodecaedro es un poliedro uniforme estrellado, indexado como U38. Tiene 54 caras (30 cuadrados, 12 pentágonos y 12 pentagramas), 120 aristas y 60 vértices.[1] Le corresponde el símbolo de Schläfli t0,2{5⁄2,5}, y según la construcción de Wythoff también puede ser denominado gran dodecaedro canteado.
| Rombidodecadodecaedro | ||
|---|---|---|
 | ||
 Modelo 3D | ||
| Tipo |
poliedro estrellado uniforme | |
| Forma de las caras |
cuadrado (30) pentagrama (12) | |
| Configuración de vértices |
trapecio | |
| Dual |
mediano hexecontaedro deltoidal | |
| Elementos | ||
| Vértices | 60 | |
| Aristas | 120 | |
| Caras | 54 | |
| Más información | ||
| MathWorld |
Rhombidodecadodecahedron | |
Coordenadas cartesianas
Las coordenadas cartesianas de los vértices de un gran rombicosidodecaedro uniforme son todas las permutaciones pares de:
- (±1/τ2, 0, ±τ2)
- (±1, ±1, ±√5)
- (±2, ±1/τ, ±τ)
donde τ = (1+√5)/2 es número áureo (a veces escrito φ).
Poliedros relacionados
Comparte su disposición de vértices con el compuesto uniforme de 10 o de 20 prismas triangulares. Además, comparte sus aristas con el icosidodecadodecaedro (que tiene en común las caras pentagonales y pentagrámicas) y con el rombicosaedro (que tiene en común las caras cuadradas).
 Envolvente convexa |
 Rombidodecadodecaedro |
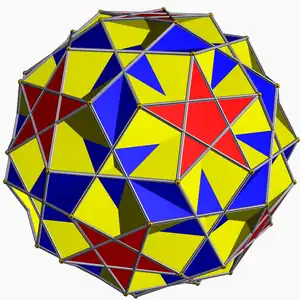 Icosidodecadodecaedro |
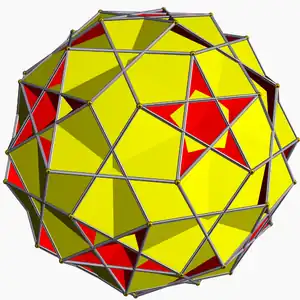 Rombicosaedro |
 Compuesto de diez prismas triangulares |
 Compuesto de veinte prismas triangulares |
Mediano hexecontaedro deltoidal
| Mediano hexecontaedro deltoidal | ||
|---|---|---|
 Imagen del sólido | ||
| Tipo | Poliedro estrellado | |
| Caras |
60 | |
| Aristas | 120 | |
| Vértices | 54 | |
| Grupo de simetría | Ih, [5,3], *532 | |
| Poliedro dual | Rombidodecadodecaedro | |

El mediano hexecontaedro deltoidal (o mediano ditriacontaedro lanceal) es un poliedro no convexo isoedral. Es el dual del rombidodecadodecaedro, y posee 60 caras cuadriláteras que se cruzan entre sí.
Véase también
Referencias
- Maeder, Roman. «38: rhombidodecadodecahedron». MathConsult.
Bibliografía
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208, doi:10.1017/CBO9780511569371.
Enlaces externos
- Weisstein, Eric W. «Rhombidodecadodecahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Medial deltoidal hexecontahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Poliedros uniformes y duales