Anexo:Galería de grafos
A continuación se lista una galería de grafos que se distinguen por su tipología o propiedades.
Familias de grafos
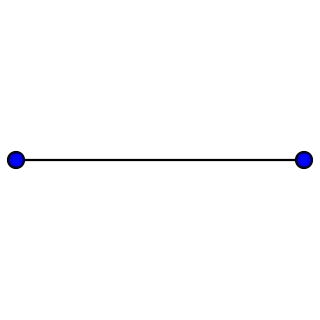
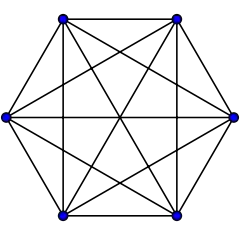
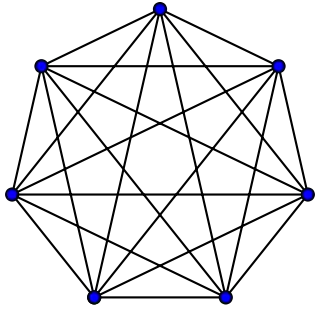
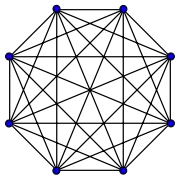
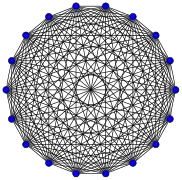
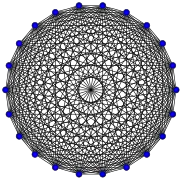
Grafos completos
El grafo completo de vértices es a menudo llamado El -clique y por lo general denotado como , del alemán komplett.[1]
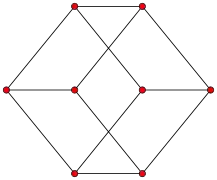
Grafos completos bipartitos
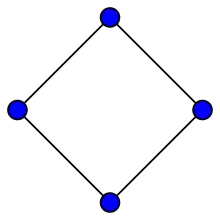
El Grafo bipartito completo es por lo general denotado . Para grafos de fórmula ver mejor la sección 1.9 grafos estrella. El grafo bipartito completo es igual que el grafo ciclo (el cuadrado) mostrado en la sección grafos ciclo.

 , grafo de Thomsen
, grafo de Thomsen







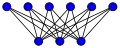
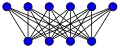
Ciclos
Los grafos cíclicos de vértices son denominados n-ciclos y generalmente son denotados como . También son llamados polígonoso n-gonos. Casos especiales son el triángulo , el cuadrado , y todos los restantes polígonos convexos, como pentágono , hexágono , etc.
Grafos de la amistad

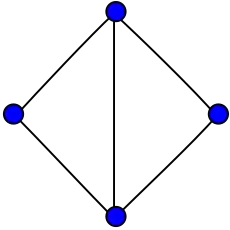
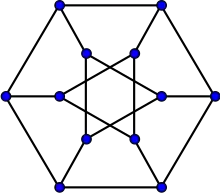
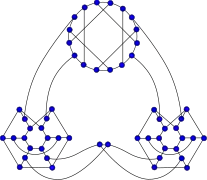
Los grafos de la amistad F2, F3 and F4.
Grafos de fullerenos
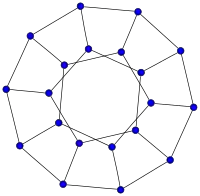
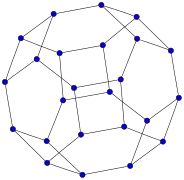
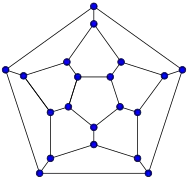 20-fullereno (grafo dodecaédrico)
20-fullereno (grafo dodecaédrico)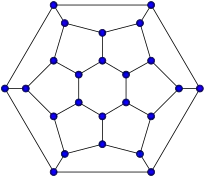 24-fullereno (grafo trapezoedro hexagonal truncado)
24-fullereno (grafo trapezoedro hexagonal truncado)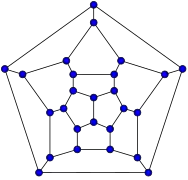 26-fullereno
26-fullereno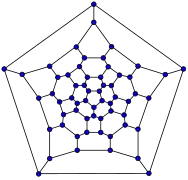 60-fullereno (grafo icosaédrico truncado)
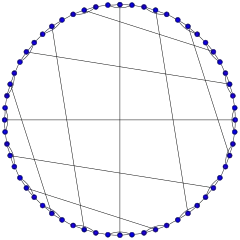
60-fullereno (grafo icosaédrico truncado)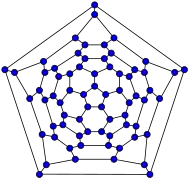 70-fullereno
70-fullereno
Sólidos platónicos
Sólidos platónicos truncados
Snarks
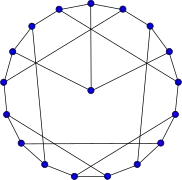 Snark de Blanuša (primero)
Snark de Blanuša (primero)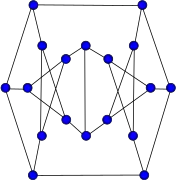 Snark de Blanuša (segundo)
Snark de Blanuša (segundo)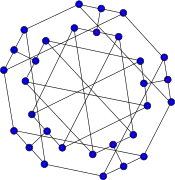 Snark doble estrellado
Snark doble estrellado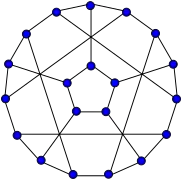 Snark flor
Snark flor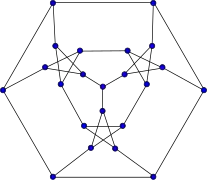 Snark de Loupekine (primero)
Snark de Loupekine (primero)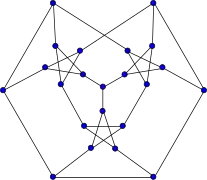 Snark de Loupekine (segundo)
Snark de Loupekine (segundo)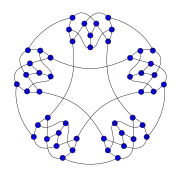 Snark de Szekeres
Snark de Szekeres Grafo de Tietze
Grafo de Tietze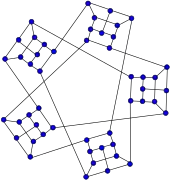 Snark de Watkins
Snark de Watkins
Estrellas

Los grafos estrellas S3, S4, S5 and S6.
Ruedas

Ruedas – .
Grafos individuales

 11-jaula de Balaban
11-jaula de Balaban
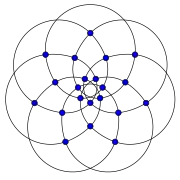 Grafo de Brinkmann
Grafo de Brinkmann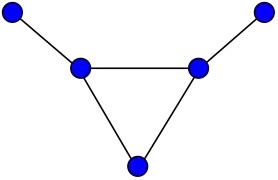

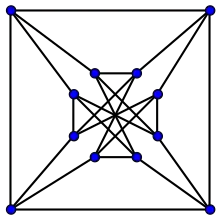
 Grafo 54 de Ellingham–Horton
Grafo 54 de Ellingham–Horton Grafo 78 de Ellingham–Horton
Grafo 78 de Ellingham–Horton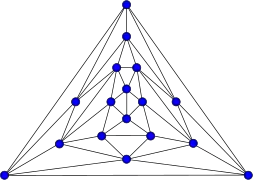 Grafo de Errera
Grafo de Errera Grafo de Franklin
Grafo de Franklin Grafo de Frucht
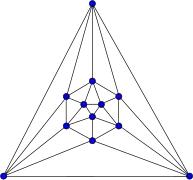
Grafo de Frucht Grafo de Goldner-Harary
Grafo de Goldner-Harary Grafo de Grötzsch
Grafo de Grötzsch Grafo de Harries
Grafo de Harries Grafo de Harries-Wong
Grafo de Harries-Wong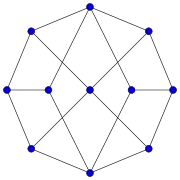 Grafo de Herschel
Grafo de Herschel Grafo de Hoffman
Grafo de Hoffman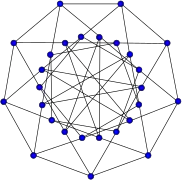 Grafo de Holt
Grafo de Holt Grafo de Horton
Grafo de Horton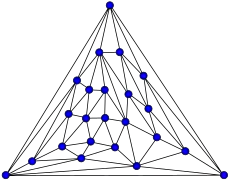 Grafo de Kittell
Grafo de Kittell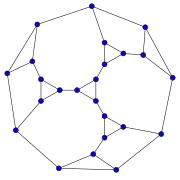 Grafo de Markström
Grafo de Markström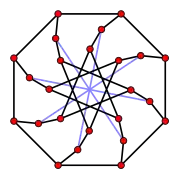
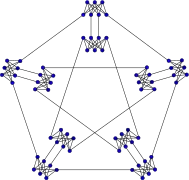 Grafo de Meredith
Grafo de Meredith Huso de Moser
Huso de Moser Grafo de Sousselier
Grafo de Sousselier Grafo de Poussin
Grafo de Poussin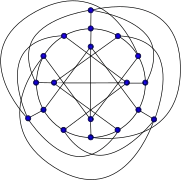 Grafo de Robertson
Grafo de Robertson Fragmento de Tutte
Fragmento de Tutte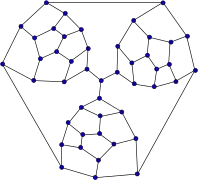 Grafo de Tutte
Grafo de Tutte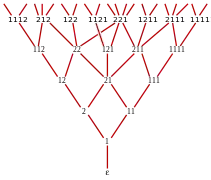 Grafo de Young–Fibonacci
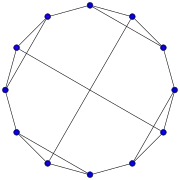
Grafo de Young–Fibonacci Grafo de Wagner
Grafo de Wagner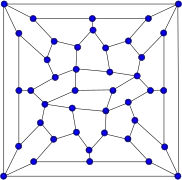 Grafo de Wiener–Araya
Grafo de Wiener–Araya
Grafos con grados de simetría
Grafos fuertemente regulares

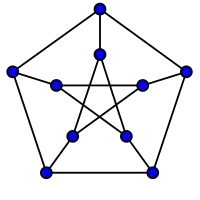
 Grafo de Hall-Janko
Grafo de Hall-Janko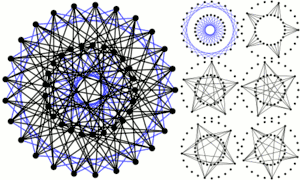 Grafo de Hoffman-Singleton
Grafo de Hoffman-Singleton Grafo de Higman-Sims
Grafo de Higman-Sims Grafo de Paley de orden 13
Grafo de Paley de orden 13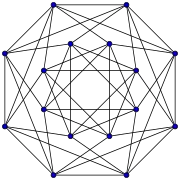 Grafo de Shrikhande
Grafo de Shrikhande Grafo de Schläfli
Grafo de Schläfli Grafo de Brouwer–Haemers
Grafo de Brouwer–Haemers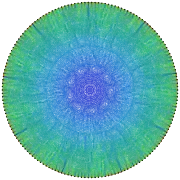 Grafo de McLaughlin local
Grafo de McLaughlin local Grafo de Perkel
Grafo de Perkel Grafo de Gewirtz
Grafo de Gewirtz
Grafos simétricos
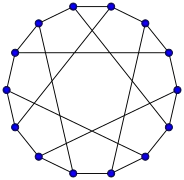
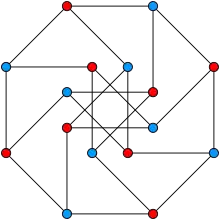
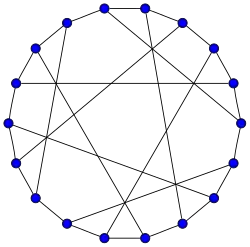
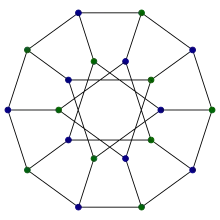
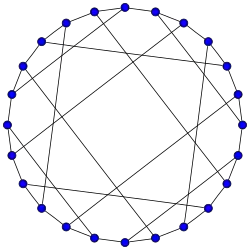


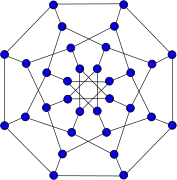
 Grafo de Foster
Grafo de Foster Grafo de Biggs-Smith
Grafo de Biggs-Smith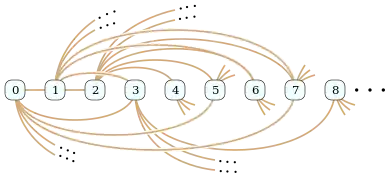 Grafo de Rado
Grafo de Rado
Grafos semi-simétricos
 Grafo de Folkman
Grafo de Folkman Grafo de Gray
Grafo de Gray Grafo de Ljubljana
Grafo de Ljubljana 12-jaula de Tutte
12-jaula de Tutte
Véase también
Referencias
- David Gries and Fred B. Schneider, A Logical Approach to Discrete Math, Springer, 1993, p 436.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Galería de grafos.
Wikimedia Commons alberga una categoría multimedia sobre Galería de grafos.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.