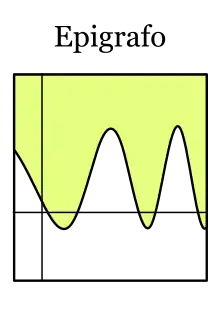
El epigrafo de una función de valor real es la zona "sobre" la curva.

En matemática, el epigrafo de una función real f : Rⁿ→R es el conjunto de puntos situados en o sobre esta:

${\displaystyle {\mbox{epi}}f=\{(x,\mu )\,:\,x\in \mathbb {R} ^{n},\,\mu \in \mathbb {R} ,\,f(x)\leq \mu \}\subseteq \mathbb {R} ^{n+1}.}$

Análogamente, el conjunto de puntos en o por debajo de esta función es un hipografo.

Cuando nos referimos a relaciones, tales como relaciones de preferencia en economía, un conjunto definido de esta manera generalmente se llama conjunto contorno superior.

Propiedades

Una función es convexa si y sólo si su epigrafo es un conjunto convexo. El epigrafo de una función afín real g : Rⁿ→R es un semiplano en Rⁿ⁺¹.

Una función es inferiormente semicontinua si y sólo si su epigrafo es cerrado.

Referencias

• Rockafellar, Ralph Tyrell (1996), Convex Analysis, Princeton University Press, Princeton, NJ. ISBN 0-691-01586-4.