Problema del diamante azteca

En combinatoria, un diamante azteca de orden n está formado por todos los cuadrados de una cuadrícula cuyos centros (x, y) satisfacen la condición de que |x| + |y| ≤ n, siendo n un número entero dado. La rejilla consiste en una serie de cuadrados de lado unidad con el origen como un vértice de 4 de ellos, de modo que tanto x como y son números semienteros.[1]

El teorema del diamante azteca indica que el número de maneras distintas posibles de recubrir con un teselado en dominó un diamante azteca de orden n es:[2]

2^n(n+1)/2

El teorema del círculo ártico afirma que un recubrimiento aleatorio de un gran diamante azteca tiende a ordenarse fuera de un cierto círculo.[3]

• 
  Diamante azteca de orden 4, con 1024 posibles recubrimientos en dominó
• 
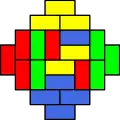  Uno de estos teselados
• 
  Teselado aleatorio con dominós de una zona hexagonal, con las teselas "congeladas" en color blanco. (Teorema del círculo ártico)

Es común colorear las fichas de la manera siguiente:

• Primero, considérese un coloreado del diamante como el de un tablero de ajedrez.
• Cada dominó cubrirá exactamente un cuadrado negro y otro blanco.
• Las teselas verticales donde el cuadrado superior cubre un cuadrado negro, se colorean de negro, y las otras teselas verticales, en un segundo color.
• Se aplica el mismo procedimiento a las teselas horizontales, con izquierda y derecha