Poliedro ditrigonal
En geometría, se denomina poliedros ditrigonales a aquellos cuya figura de vértice posee simetría hexagonal. Existe un total de siete poliedros uniformes y poliedros duales uniformes, denominados ditrigonales.[1]
Figuras de vértice ditrigonales
Existen cinco poliedros uniformes ditrigonales, todos con simetría icosaédrica.[1]
Los tres poliedros uniformes estrellados con símbolo de Wythoff de la forma 3 | p'q o 32 | p'q son ditrigonales, al menos si p y q no son 2. Cada poliedro incluye dos tipos de caras, siendo triángulos, pentágonos, o estrellas pentagonales. Sus configuraciones de vértices tienen la forma p.q.p.q.p.q o (p.q)3 con una simetría de orden 3. Aquí, el término ditrigonal se refiere a un hexágono que tiene una simetría de orden 3 (simetría triangular) que actúa con 2 órbitas de rotación en los 6 ángulos de la figura de vértice (la palabra ditrigonal significa "que tiene dos conjuntos de 3 ángulos").[2]
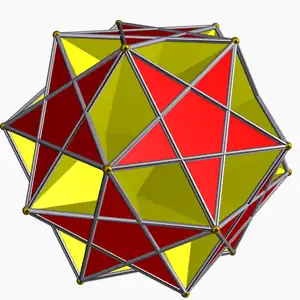
| Tipo | Pequeño icosidodecaedro ditrigonal | Dodecadodecaedro ditrigonal | Gran icosidodecaedro ditrigonal |
|---|---|---|---|
| Imagen | 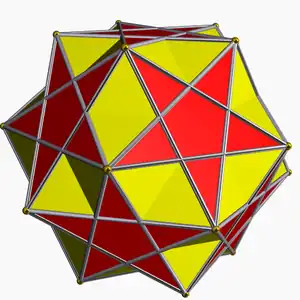 |
 |
 |
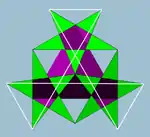
| Figura de vértice | 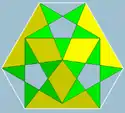 |
 |
 |
| Configuración de vértices | 3.5⁄2.3.5⁄2.3.5⁄2 | 5.5⁄3.5.5⁄3.5.5⁄3 | (3.5.3.5.3.5)/2 |
| Caras | 32 20 {3}, 12 {5⁄2 } |
24 12 {5}, 12 {5⁄2 } |
32 20 {3}, 12 {5} |
| Símbolo de Wythoff | 3 | 5/2 3 | 3 | 5/3 5 | 3 | 3/2 5 |
| Diagrama de Coxeter-Dynkin |
Otros poliedros ditrigonales uniformes
El pequeño dodecicosidodecaedro ditrigonal y el gran dodecicosidodecaedro ditrigonal también son uniformes.
Sus duales son respectivamente el pequeño hexecontaedro dodecacrónico ditrigonal y el gran hexecontaedro dodecacrónico ditrigonal.[1]
Véase también
- Pequeño icosidodecaedro complejo
- Gran icosidodecaedro complejo
Referencias
- Har'El, 1993
- Uniform Polyhedron, Mathworld (retrieved 10 June 2016)
Bibliografía
- Coxeter, H.S.M., M.S. Longuet-Higgins y J.C.P Miller, Uniform Polyhedra, Phil. Trans. 246 A (1954) págs. 401–450.
- Har'El, Z. Solución uniforme para uniforme Polyhedra., Geometriae Dedicata 47, 57–110, 1993. Zvi Har' El, Kaleido software, org/web/20110520080303/http://www.math.technion.ac.il/~rl/kaleido/poly.html Imágenes, www.math.technion.ac.il/~rl/kaleido/dual.html imágenes duales
Lecturas adicionales
- Johnson, N.; The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Skilling, J. (1975), «The complete set of uniform polyhedra», Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 278 (1278): 111-135, ISSN 0080-4614, JSTOR 74475, MR 0365333, S2CID 122634260, doi:10.1098/rsta.1975.0022.