Nudo primo
En teoría de nudos, un nudo primo o eslabón primo es un nudo que es, en cierto sentido, indescomponible. Específicamente, es un nudo no trivial que no puede describirse como la suma conexa de dos nudos no triviales. Los nudos que no son primos se denominan nudos compuestos o enlaces compuestos. Puede ser un problema no trivial determinar si un nudo dado es primo o no.
Propiedades
Una familia de ejemplos de nudos primos son los nudos tóricos, que se forman envolviendo un toro haciendo pasar un cordel por su agujero central para enrollarlo p veces en un sentido y q veces en el otro, cuando p y q son números enteros coprimos.
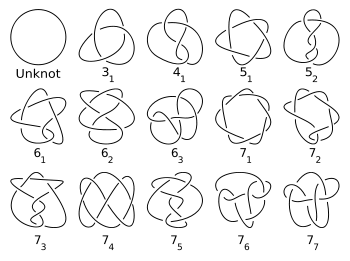
El nudo principal más simple es el trébol, con tres cruces, que es en realidad un nudo toroide (2, 3). El nudo en ocho, con cuatro cruces, es el nudo sin toroide más simple. Para cualquier número entero n positivo, hay un número finito de nudos primos con n cruces. Los primeros valores (sucesión A002863 en OEIS) se dan en la siguiente tabla:
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Número de nudos primos
con n cruces0 0 1 1 2 3 7 21 49 165 552 2176 9988 46972 253293 1388705 Nudos compuestos 0 0 0 0 0 2 1 4 ... ... ... ... Total: (sucesión A002863 en OEIS) 0 0 1 1 2 5 8 25 ... ... ... ...
Los casos de nudos enantiomorfos se cuentan solo una vez en esta tabla y en el siguiente cuadro (es decir, un nudo y su imagen especular se consideran equivalentes).
Teorema de Schubert
Un teorema debido a Horst Schubert establece que cada nudo puede expresarse de manera única como una suma conexa de nudos primos.[1]
Véase también
Referencias
- Schubert, H. "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten". S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
Enlaces externos
- Weisstein, Eric W. «Prime Knot». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- "Prime Links with a Non-Prime Component", The Knot Atlas
| Control de autoridades |
|
|---|
Datos: Q1014491
Multimedia: Prime knots and links / Q1014491