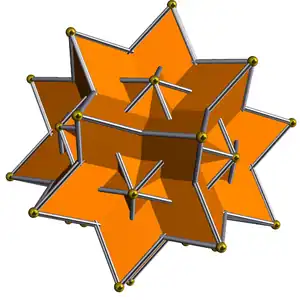
Gran triacontaedro rómbico

Forma de las caras

Se puede construir a partir del sólido convexo expandiendo las caras por el factor de ${\displaystyle \varphi ^{3}\approx 4.236}$; donde ${\displaystyle \varphi \!}$ es el número áureo.

Los rombos tienen dos ángulos de ${\displaystyle \arccos({\frac {1}{5}}{\sqrt {5}})\approx 63.434\,948\,822\,92^{\circ }}$ y dos de ${\displaystyle \arccos(-{\frac {1}{5}}{\sqrt {5}})\approx 116.565\,051\,177\,08^{\circ }}$. Su ángulo diedro es igual a ${\displaystyle \arccos(-{\frac {1}{4}}+{\frac {1}{4}}{\sqrt {5}})=72^{\circ }}$. Parte de cada rombo se encuentra dentro de la figura, por lo que no son totalmente visibles en los modelos sólidos. La relación entre las longitudes de la diagonal larga y corta de los rombos es igual a la proporción áurea ${\displaystyle \varphi }$.

Este sólido es al compuesto de gran dodecaedro estrellado y gran icosaedro lo que el correspondiente sólido convexo es al compuesto de dodecaedro e icosaedro. Las aristas que se cruzan en el politopo compuesto son las diagonales de los rombos.

En el centro de este compuesto se puede ver lo que se asemeja a un triacontaedro rómbico "excavado" (compárese con el dodecaedro excavado y con el icosaedro excavado). El resto del poliedro se parece sorprendentemente a un hexecontaedro rómbico.

Triacontaedro convexo, mediano y gran rómbico a la derecha (mostrado con simetría tetraédrica) y los politopos compuestos correspondientes de sólidos regulares a la izquierda	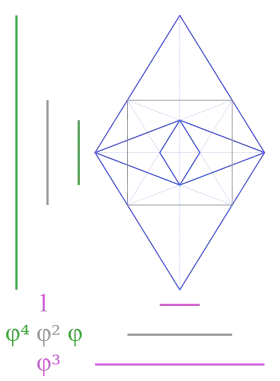Las longitudes diagonales de las caras de los tres triacontaedros rómbicos son potencias de ${\displaystyle \varphi }$
	Proyecciones ortográficas según ejes de simetría de 2, 3 y 5 lóbulos

• Weisstein, Eric W. «Great rhombic triacontahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
• David I. McCooey: animación y medidas
• Poliedros uniformes y duales