Estimador extremo

Un estimador ${\displaystyle {\hat {\theta }}}$ se llama estimador extremo si existe una función objetivo ${\displaystyle {\hat {Q}}_{n}}$ tal que

${\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\;max} }}\ {\widehat {Q}}_{n}(\theta ),}$

donde ${\displaystyle \Theta }$ es el espacio de parámetros. A veces se da una condición más débil:

${\displaystyle {\widehat {Q}}_{n}({\hat {\theta }})\geq \max _{\theta \in \Theta }\,{\widehat {Q}}_{n}(\theta )-o_{p}(1),}$

donde ${\displaystyle o_{p}(1)}$ es una variable que converge en probabilidad a cero. Con esta modificación, ${\displaystyle {\hat {\theta }}}$ no necesita ser el valor exacto que maximiza la función objetivo, sino simplemente estar lo suficientemente cerca de ese valor.

La teoría de los estimadores extremos no especifica cuál debe ser la función objetivo. Existen varios tipos de funciones objetivo adecuadas para diferentes modelos, por lo que el estudio de los estimadores extremos nos permite analizar simultáneamente las propiedades teóricas de una amplia clase de estimadores. La teoría sólo especifica las propiedades que la función objetivo debe tener, de forma que, cuando uno elige una función objetivo particular, sólo debe verificar que esas propiedades se cumplen.

Cuando el espacio de parámetros ${\displaystyle \Theta }$ no es compacto (${\displaystyle \Theta =\mathbb {R} }$ en este ejemplo), aunque la función objetivo tenga un único máximo en ${\displaystyle \theta _{0}}$, este máximo puede no estar bien separado, en cuyo caso el estimador ${\displaystyle {\hat {\theta }}}$ no será consistente.

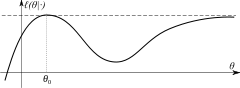
Si el espacio de parámetros ${\displaystyle \Theta }$ es compacto y existe una función límite ${\displaystyle Q_{0}(\theta )}$ tal que:

1. ${\displaystyle {\hat {Q}}_{n}(\theta )\rightarrow Q_{0}(\theta )}$ en probabilidad uniformemente en ${\displaystyle \Theta }$, y
2. la función ${\displaystyle Q_{0}(\theta )}$ es continua y tiene un único máximo en ${\displaystyle \theta =\theta _{0}}$,

entonces ${\displaystyle {\hat {\theta }}}$ es un estimador consistente de ${\displaystyle \theta _{0}}$.[1]

La convergencia uniforme en probabilidad de ${\displaystyle {\hat {Q}}_{n}(\theta )}$ significa que

${\displaystyle \sup _{\theta \in \Theta }{\big |}{\hat {Q}}_{n}(\theta )-Q_{0}(\theta ){\big |}\ {\xrightarrow {p}}\ 0.}$

La condición de que ${\displaystyle \Theta }$ sea compacto puede relajarse: basta suponer que el máximo de ${\displaystyle Q_{0}}$ está bien separado, es decir, que para toda secuencia ${\displaystyle \{\theta _{i}\}}$ tal que ${\displaystyle Q_{0}(\theta _{i})\rightarrow Q_{0}(\theta _{0})}$ se verifica ${\displaystyle \theta _{i}\rightarrow \theta _{0}}$. Intuitivamente, esto significa que no existen puntos ${\displaystyle \theta }$ lejanos a ${\displaystyle \theta _{0}}$ tales que ${\displaystyle Q_{0}(\theta )}$ esté próximo a ${\displaystyle Q_{0}(\theta _{0})}$.

Suponiendo que son ciertas las hipótesis anteriores para la consistencia y que las derivadas de ${\displaystyle {\hat {Q}}_{n}}$ satisfacen ciertas condiciones,[2] el estimador extremo es asintóticamente normal.

• La estimación por máxima verosimilitud utiliza la función objetivo

${\displaystyle {\hat {Q}}_{n}(\theta )=\log \left[\prod _{i=1}^{n}f(x_{i}|\theta )\right]=\sum _{i=1}^{n}\log f(x_{i}|\theta ),}$

donde ${\displaystyle f(\cdot |\theta )}$ es la función de densidad de la distribución de la que fue extraída la muestra. Esta función objetivo se llama función de log-verosomilitud.

• El estimador del método de los momentos generalizado se define mediante la función objetivo

${\displaystyle {\hat {Q}}_{n}(\theta )=-{\Bigg (}{\frac {1}{n}}\sum _{i=1}^{n}g(x_{i},\theta ){\Bigg )}'{\hat {W}}_{n}{\Bigg (}{\frac {1}{n}}\sum _{i=1}^{n}g(x_{i},\theta ){\Bigg )}.}$

• Estimador de mínima distancia.